Tutorial ini ditujukan untuk mengetahui dengan cepat penggunaan dari Tensorflow. Jika Anda ingin mempelajari lebih dalam terkait tools ini, silakan Anda rujuk langsung situs resmi dari Tensorflow dan juga berbagai macam tutorial yang tersedia di Internet. Saat ini, ada sangat banyak materi online terkait hal ini.

Jika kita mendengar kata "tensorflow", sebagian besar dari kita akan langsung mengaitkan dengan istilah "deep learning". Padahal, tensorflow sebenarnya adalah tools untuk melakukan komputasi numerik (lebih luas daripada hanya sekedar untuk deep learning). Contoh-contoh task terkait komputasi numerik adalah seperti mengerjakan operasi matriks, melakukan (convex) function optimization, menghitung gradient atau hessian (turuan kedua) dari sebuah fungsi, dsb. Isu-isu yang ada di deep learning, seperti representation learning, optimization, operasi matriks dan tensor, adalah proses komputasi numerik yang dapat dilakukan dengan tensorflow. Selain tensorflow, ada banyak tools yang serupa seperti MATLAB, Octave, Numpy, Scipy, dsb. Namun, tensoflow menawarkan berbagai macam kelebihan, yang utama adalah seperti kemampuan untuk melakukan komputasi yang memanfaatkan banyak CPUs dan GPUs.

Hal pertama yang perlu dipahami ketika ingin menggunakan tensorflow adalah konsep computational graph. Anda bisa membaca Colah's blog untuk memahami hal ini dalam hal neural networks. Di tensorflow, graf dibentuk dari 2 komponen berikut:

• Node merepresentasikan operasi matematika/numerik
• Sisi merepresentasikan aliran tensor (bentuk umum dari matriks, maupun vektor)

Sebagai contoh, operasi matematika: y = a^2 + (b \times c) dapat divisualisasikan dengan computational graph berikut.

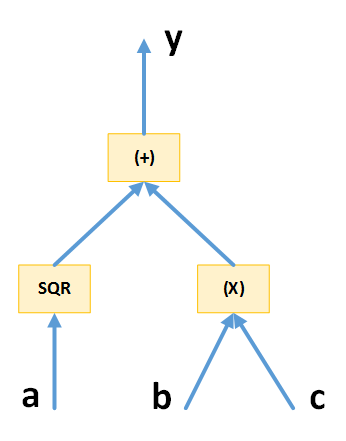
Kita langsung saja praktikum pengenalan tensorflow untuk membuat graf komputasi dan bagaimana mengeksekusi graf komputasi tersebut. Pertama, kita perlu import tensorflow dan juga numpy (digunakan kita menggunakan graf komputasi dengan placeholder).

import tensorflow as tf
import numpy as np

Kemudian, kita akan mencoba untuk membuat sebuah graf komputasi sederhana sebagai berikut.

## contoh 1: membuat computational graph sederhana (tanpa input dengan placeholder)

x = tf.constant(5)
y = x + 1

Perhatikan bahwa x, y, 1, dan 5 adalah tensor dengan masing-masing mempunyai dimensi R^1. Anda pasti dapat dengan mudah membayangkan visualisasi graf seperti apa yang dapat ditampilkan dengan graf di atas. Jika Anda mencoba untuk mencetak nilai y ke layar dengan perintah berikut, nilai 6 tidak akan muncul di layar. Ini karena y adalah object tensor.

# tidak akan muncul 6, y hanyalah graph komputasi
print (y)

Jika Anda ingin eksekusi graf komputasi yang bermuara pada tersebut, gunakan potongan kode berikut:

# kalau mau eksekusi, gunakan Session, lalu run
with tf.Session() as sess:
    y_ = sess.run(y)
    print (y_)

Contoh berikut adalah contoh operasi yang melibatkan tensor dengan dimensi (shape) yang lebih tinggi. Pada contoh di bawah, W \in R^{3 \times 2}, u \in R^{2 \times 1}, dan v \in R^{3 \times 1}

# contoh lain untuk perkalian matrix-vector

W = tf.constant([[1,1],[2,2],[3,3]]) # shape W : (3, 2)
u = tf.constant([[2],[1]]) # shape u : (2,1)

# tf.matmul(., .) adalah operasi perkalian matriks
v = tf.matmul(W, u) # harusnya shape v : (3, 1)

with tf.Session() as sess:
    print (sess.run(v))

Placeholder sebagai Input ke Graf Komputasi

Pada contoh sebelumnya, input dari graf komputasi bersifat konstan. Jika kita hanya ingin membuat graf komputasi tanpa bergantung dengan isi input, kita dapat menggunakan placeholder. Placeholder nantinya akan diisi dengan nilai tensor yang sesungguhnya ketika kita akan mengeksekusi graf tersebut.

## contoh 2: membuat computational graph sederhana (dengan input dengan placeholder)
## jadi, input ke graph komputasi bisa diganti-ganti, namun graphnya tetap satu

# beberapa jenis input yang berbeda-beda
# input dalam bentuk Numpy Array
data_1 = np.array([[2,3],[3,1]])
data_2 = np.array([[4,8],[1,8]])

# buat graph

# membuat placeholder dengan shape (2,2)
M = tf.placeholder(shape=[2, 2], dtype=tf.int32)

N = tf.constant([[1,0],[0,1]])
Z = tf.matmul(M, N)

Pada contoh di atas, placeholder M merupakan penampung yang nantinya hanya bisa diisi dengan tensor yang mempunyai dimensi M \in R^{2 \times 2}. Sekarang, jika kita ingin eksekusi graf tersebut, kita wajib mengisi placeholder M dengan sebuah nilai yang shape/dimensi sudah ditentukan. Pengisian dilakukan melalui dictionary yang di-pass saat memangil sess.run(.).

# coba jalankan dengan ganti M dengan nilai yang ingin dimasukkan
with tf.Session() as sess:
    print (sess.run(Z, feed_dict={M: data_1}))
    print (sess.run(Z, feed_dict={M: data_2}))

Gradient-based Optimization (Gradient Descent)

Salah satu manfaat dari tensorflow adalah untuk optimasi fungsi. Misal, kita diberikan permasalahan berikut: carilah nilai x, sehingga F(x) = 2x^4 + x^3 + 3x^2 mencapai titik local minima (syukur-syukur bisa global minima :)). Sebelumnya, kita sudah mengetahui bahwa salah satu framework yang dapat digunakan untuk permasalahan optimasi ini adalah dengan metode gradient descent, yaitu kita mencoba melakukan beberapa kali iterasi untuk melakukan update berikut:

Dimana \theta adalah parameter yang ingin dicari nilainya agar fungsi F(\theta) menjadi optimum (dalam hal ini local minima), dan \alpha adalah learning rate.

Pertama-tama, kita import terlebih dahulu Numpy dan Tensorflow.

import tensorflow as tf
import numpy as np

Lalu, kita rakit terlebih dahulu graf komputasi yang berupa fungsi yang ingin kita optimasi. Disini, kita membutuhkan konsep variable pada tensorflow, yaitu trainable parameter/variable yang justru nilai-nya berubah-ubah dan ingin kita cari agar fungsi utama menjadi optimal.

#### step 1: rakit dahulu fungsi yang mau di-optimasi ####

# x adalah trainable parameter/variable
# x hanyalah sebuah bilangan R --> tensor dengan dimensinya hanya (1,) -> [1]
x = tf.get_variable("par_x", [1], initializer=tf.random_uniform_initializer(minval=-2, maxval=2))

# rakit fungsi yang mau dioptimasi
# INGAT !!! INI HANYA COMPUTATIONAL GRAPH! BUKAN LANGSUNG DIEKSEKUSI !!!
f = (2*x*x*x*x) + (x*x*x) - (3*x*x)

Berikutnya, kita definisikan optimizer yang akan kita gunakan, yaitu Gradient Descent Optimizer seperti yang sudah kita pelajari sebelumnya. Perhatikan bahwa kita tidak perlu "repot" membangun proses komputasi untuk menghitung gradient (turunan parsial) dari fungsi utama terhadap parameter karena semuanya sudah dilakukan oleh tensorflow. Kita hanya perlu membangun graf komputasi untuk proses satu step update.

#### step 2: buat optimizer-nya --> SGD
# pakai SGD, learning_rate = 0.01
optimizer = tf.train.GradientDescentOptimizer(0.05)

# komputasi untuk sekali update, satu step menuju local minimal (arah ditentukan oleh gradient)
train_onestep = optimizer.minimize(f) #tuliskan siapa yang mau di-optimasi

Kemudian, kita definisikan sebuah fungsi untuk melakukan training dan mencari nilai x yang diinginkan. Di dalam fungsi tersebut, ada sebuah loop sebanyak epoch kali untuk melakukan update terhadap nilai variable/parameter sehingga fungsi menuju local optima.

#### step 3: bangun fungsi trainer --> loop berulang-ulang --> Gradient-based optimization ####
def train(sess, epoch=50):

    # jalankan inisialisasi random parameter awal
    # di tensorflow, jika ada trainable parameter, ini WAJIB dilaksanakan terlebih dahulu!
    init = tf.global_variables_initializer()
    sess.run(init)

    #mulai epoch
    for i in range(epoch):

        # update 1 langkah menuju local optima!
        _, curr_f_x, curr_x = sess.run([train_onestep, f, x])

        #cetak progress untuk setiap 'step' epoch
        print ("\r Epoch-{}, F(x)-value: {}, x-value: {}".format(i+1, curr_f_x, curr_x))

Terakhir, dengan scope Session, kita lakukan training dengan memanggil fungsi train(.) tersebut. Sekalian setelah itu, kita tampilkan nilai parameter/variable x yang harapannya membuat fungsi F(x) minimal.

#### step 4: laksanakan training & setelah itu tampilkan siapa x yang berhasil membuat f(x) optimal
with tf.Session() as sess:

    ### training ###
    train(sess)
    
    ### tampilkan siapa x itu; X yang terakhir setelah training! ###
    print (sess.run(x))

Di salah satu kesempatan, mungkin Anda akan mendapatkan proses optimasi fungsi seperti pada visualisasi berikut:

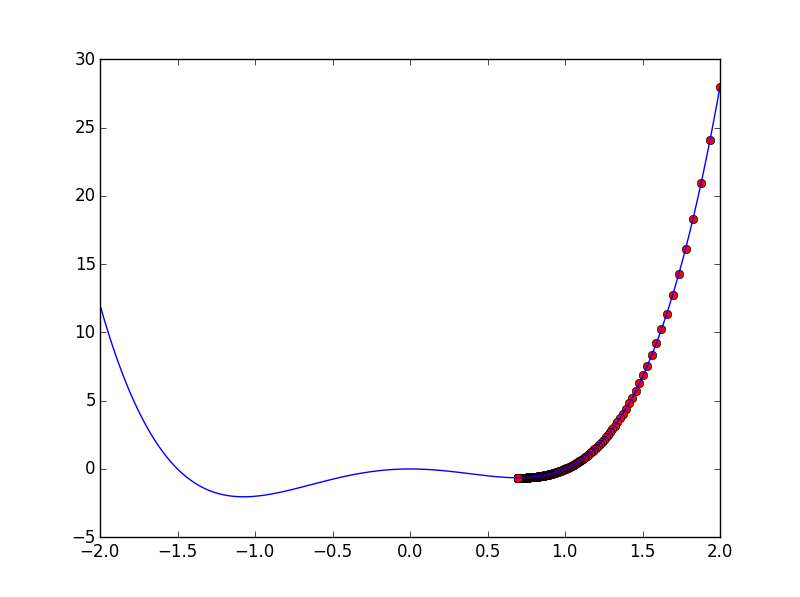
.:LATIHAN:.
Coba cari nilai x,y sehingga fungsi f(x,y) = 50 - x^2 - 2y^2 mencapai local maximum!

Implementasi Logistic Regression Model

Setelah Anda memahami konsep dasar dari tensorflow dan Anda memahami langkah-langkah untuk melakukan optimasi fungsi dengan API yang disediakan oleh tensorflow, kita saatnya Anda mencoba untuk membangun model machine learning tradisional yang sangat terkenal, yaitu logistic regression. Tutorial kali ini mengasumsikan Anda sudah mengikuti kuliah kami terkait logistic regression sebelumnya, atau dari kuliah-kuliah yang lain. Pertama, kita review terlebih dahulu terkait logistic regression. Secara umum, logistic regression biasanya digunakan untuk melakukan pekerjaan binary classification. Misal, diberikan sebuah input berupa kalimat x, kita ingin mencari fungsi klasifikasi sentiment dari kalimat tersebut, yaitu F(x; \theta), dimana 0 \leq F(x; \theta) \leq 1 sehingga F(x; \theta) \leq 0.5 jika kalimat tersebut mempunyai sentiment negatif, dan F(x; \theta) > 0.5 jika positif. Secara umum, fungsi klasifikasi dinyatakan dengan

Dimana W dan b adalah parameter yang ingin dicari agar fungsi klasifikasi tersebut berhasil bekerja dengan performa terbaik.

Ingat bahwa fungsi yang akan kita optimasi dalam hal ini bukanlah fungsi F(x; W,b), tetapi loss function yang mengukur seberapa dekat output dari fungsi dengan output sesungguhnya yang diharapkan. Misal, output dari fungsi dinotasikan dengan y = F(x; W,b), dan output yang diharapkan (nilai sesungguhnya) adalah y', loss function yang dapat kita gunakan (dan yang akan kita optimasi) adalah cross entropy yaitu:

Jadi, ketika kita melakukan optimasi fungsi loss tersebut, kita akan melakukan proses update berikut untuk setiap langkah pada proses gradient descent.

Kemudian, untuk kemudahan saat implementasi dengan tensorflow (yang merupakan operasi tensor), terkadang kita perlu sedikit melakukan trik untuk merepresentasikan fungsi F(x; W,b). Saat menjalankan proses optimasi, kita akan menggunakan mini-batch gradient descent, yaitu dalam sekali update kita gunakan beberapa sampel untuk perhitungan loss function.

dimana,

• x \in R^{B \times N}
• W \in R^{N \times 1}
• b \in R^{1}
• y \in R^{B \times 1}
• B adalah ukuran sebuah batch
• N adalah banyaknya fitur untuk sebuah instance

Kita langsung saja kepada implementasi logistic regression tersebut. Pertama-tama, kita buat dahulu data dummy untuk model logistic regression kita kali ini.

# implementasi logistic regression sederhana
# y = f(x|W,b) = sigmoid(w_1 * x_1 + ... + w_n * x_n + b)
# 
# parameter W dan b
# W adalah tensor 2D (num_fitur, 1), b adalah bilangan ril (1,)
#
# misal, y_ adalah label yang sesungguhnya
# fungsi yang dioptimasi adalah L(y, y_) = cross_entropy(y, y_)
#                                        = cross_entropy(f(x|W,b), y_)
#
# jadi, agar loss-function kita bisa dihitung, perlu 2 informasi: x, y_
# yaitu sample

# data dummy --> fitur dan label
# fitur ---> (num_sample, num_fitur)
data_x = np.array([[1,0,1,1,1,0],\
                   [0,0,0,1,1,1],\
                   [1,1,1,0,0,0],\
                   [0,1,0,1,0,0]])

# label ---> (num_sample,)
data_y_ = np.array([[1],[1],[0],[0]])

Berikutnya config variable mungkin perlu kita letakkan di atas agar jika ada modifikasi dari sisi nilai ini, program tidak terlalu banyak berubah.

# config vars
num_batch = 2
num_fitur = 6

Berikutnya adalah mendifinisikan parameter atau trainable parameter yang sudah kita bahas sebelumnya.

#### step 1: rakit fungsi yang mau di-optimasi, yaitu loss_function
# yang melibatkan f(x|W,b)

# trainable parameters, yaitu W dan b
# W -> (num_fitur, 1)
W = tf.get_variable("weights", \
                    [num_fitur, 1], \
                    initializer=tf.truncated_normal_initializer(stddev=0.02))

b = tf.get_variable("bias", \
                    [1], \
                    initializer=tf.constant_initializer(0.0))

Lalu, kita rakit graf komputasi untuk menghitung fungsi klasifikasi dan juga loss function yang akan kita optimasi untuk mencari nilai parameter yang tepat.

# dikatakan sebelumnya loss function L(y, y_) membutuhkan x agar bisa dihitung
# x berasal dari luar (yaitu data_x)
# agar x bisa dimasukkan ke graph komputasi kita, kita perlu jadikan x sebagai placeholder
# yang nantinya akan diisi dengan data_x ketika kita jalankan graph komputasi-nya
# ingat kita isi x batch demi batch (mini-batch gradient descent)
x = tf.placeholder(shape=[num_batch, num_fitur], dtype=tf.float32)

# hal serupa juga perlu untuk y_, karena akan diisi data_y_ dari luar graph
y_ = tf.placeholder(shape=[num_batch, 1], dtype=tf.float32)

# fungsi classifier f(x|W,b); namun hanya logits saja, tanpa sigmoid
y = tf.matmul(x, W) + b

# barulah kita definisikan Loss function kita
# tidak perlu khawatir, TensorFlow sudah menyediakan fungsi cross-entropy
L = tf.nn.sigmoid_cross_entropy_with_logits(labels=y_, logits=y)

Langkah berikutnya adalah mendifinisikan optimizer seperti saat sebelumnya Anda belajar mengenai optimasi fungsi secara umum.

#### step 2: buat optimizer-nya --> GD
# pakai GD, learning_rate = 0.01
optimizer = tf.train.GradientDescentOptimizer(0.05)
train_onestep = optimizer.minimize(L) #tuliskan siapa yang mau di-optimasi

Kemudian, untuk kebutuhkan training nantinya, kita memerlukan sub-program yang mengambil batch demi batch sample dari kumpulan training data kita.

#### step 3: bangun fungsi trainer --> loop berulang-ulang --> Gradient-based optimization ####

# fungsi ini digunakan saat training untuk mengambil batch demi batch pada sample
# asumsi: pastikan num_sample % num_batch = 0, artinya num_sample adalah kelipatan dari num_batch
def gen_batch(x, y, batch_size=2):
    num_sample, vector_size = x.shape

    i = 0
    while i <= num_sample - batch_size:
        yield x[i:(i+batch_size),:], y[i:(i+batch_size)]
        i = i + batch_size

Kemudian, kita gunakan fungsi untuk memuat batch demi batch tersebut dalam sebuah loop untuk update parameter melalui gradient fungsi loss terhadap parameter tersebut (mini batch gradient descent).

def train(sess, epoch=300):

    #jalankan inisialisasi random parameter awal
    init = tf.global_variables_initializer()
    sess.run(init)

    #mulai epoch
    for i in range(epoch):

        # untuk setiap batch (batch demi batch pada sample)
        for xx, yy_ in gen_batch(data_x, data_y_, batch_size=num_batch):

            # update 1 langkah!
            # INGAT ! placeholder x dan y_ perlu diisi! kalau tidak loss function tidak bisa dihitung!!
            _, loss = sess.run([train_onestep, L], feed_dict={x: xx, y_: yy_})

        #cetak progress untuk setiap 'step' epoch
        print ("Epoch-{}, loss-value: {}".format(i+1, loss))

Setelah kita membuat fungsi untuk melakukan training, kita mungkin perlu membuat fungsi untuk melakukan prediksi sebuah instance setelah semua parameter di-learn.

# fungsi berikut digunakan untuk prediksi nilai probabilitas/output untuk instances
def predict(sess, data_x):
    # scope None artinya scope default
    # reuse kembali W dan b yang sudah di-learn dari proses training sebelumnya
    # definisikan ulang graph komputasi agar x muat untuk semua instances di data_x
    x = tf.placeholder(shape=[len(data_x), num_fitur], dtype=tf.float32)
    out = tf.nn.sigmoid(tf.matmul(x, W) + b)

    # eksekusi graph, dengan x di-feed oleh data_x
    return sess.run(out, feed_dict={x: data_x})

Terakhir, kita lakukan jalankan fungsi training tersebut, dan setelahnya kita coba beberapa instance dan melihat nilai yang di-prediksi.

#### step 4: laksanakan training & setelah itu tampilkan siapa x yang berhasil membuat f(x) optimal
with tf.Session() as sess:

    ### training ###
    train(sess)

    ### coba prediksi nilai untuk training data ###
    other_data_x = np.array([[1,0,1,1,1,0],\
                             [0,0,0,1,1,1],\
                             [0,0,0,1,0,1],\
                             [1,1,1,0,0,0],\
                             [1,1,1,0,1,0],\
                             [0,1,0,1,0,0]])

    print (predict(sess, other_data_x))